近场定位问题,原文链接RIS-Aided Near-Field Localization and Channel Estimation for the Terahertz System,潘老师看到的话帮我结算一下广告费。本文已经正式出版在IEEE期刊,此处引用已标注出处,仅作学术交流用途,如需有下载/传播需求请尊重原文版权。
前言
由于近场信道建模几乎只依赖物体位置,尤其是对于太赫兹系统而言,因为其除了LoS路径以外的其他多径的环境吸收严重,定位用户终端就相当于完全掌握了传输环境。在近场和太赫兹的双重约束下,定位的作用甚至超越信道估计。如果在远场,这种问题将会退化为单参数估计,但是在近场这个估计问题相当复杂。物体在近场区的距离与角度信息(或者直角坐标下的双位置坐标)总是耦合的,难以处理。
本文作者的贡献在于利用二阶泰勒近似简化球面波传输模型,并进一步解耦了距离和角度,实现了该场景下较为高效精确的定位。
系统模型
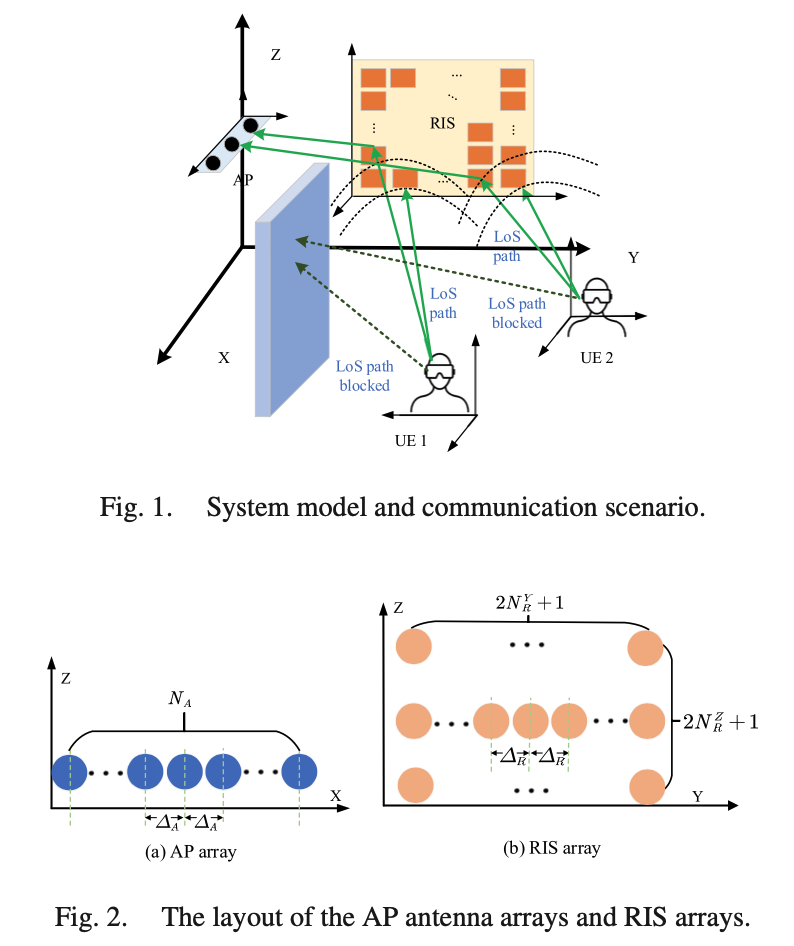
本文考虑的系统模型均为较为基础的通信假设,例如上行定位、用户单天线等。由于基站天线数量有限,很难实现高精度的定位估计,因此考虑有大型无源阵列的辅助。基本的系统模型假设如图
假设UE-RIS链路是LoS的,UE到RIS每一个阵元的距离假设为$d_{R, u}^m$,则子带$i$上接收到的信号为
\begin{equation}
\boldsymbol{a}_{R, u}^i[m]=\exp \left(-j \frac{2 \pi}{\lambda_i}\left(d_{R, u}^m-d_u^0\right)\right)
\end{equation}
增益$g_{R,u}^i$此处单独建模,并作为带估计参数,有信道建模
\begin{equation}
{\bf h}_{R, u}^i = g_{R, u}^i {\mathbf a}_{R, u}^i
\end{equation}
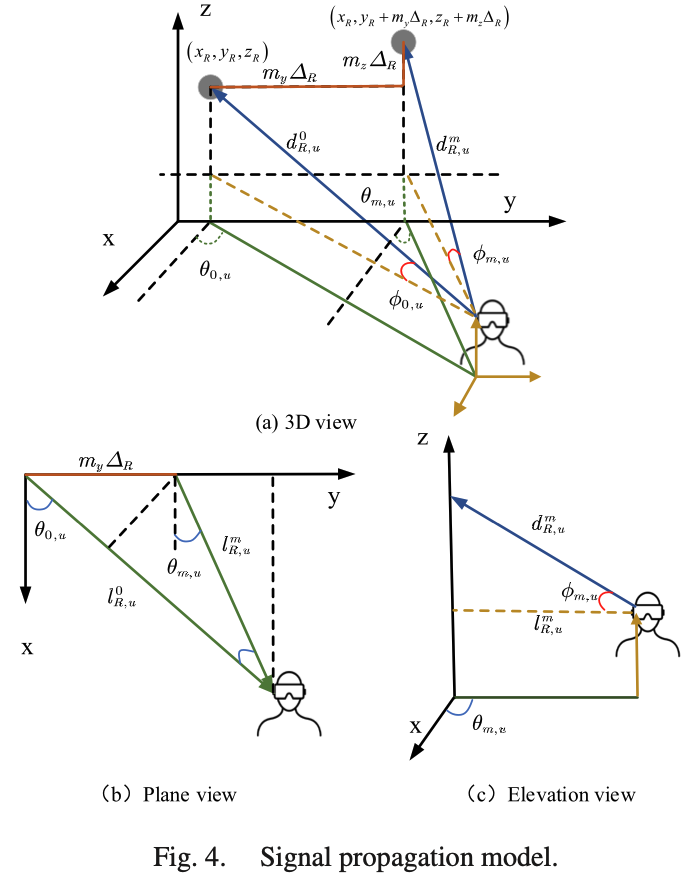
值得一提的是,关于距离和角度的参考模型如图。后续的角度计算均基于此图的定义。
图示中距离$l_{R,u}^m$的定义为$l_{R, u}^m=\sqrt{\left(m_y \Delta_R\right)^2+\left(l_{R, u}^0\right)^2-2 \sin \theta_{u, 0} m_y \Delta_R l_{R, u}^0}$,在此基础上我们可以继续计算实际距离
\begin{equation}
\begin{aligned}
d_{R, u}^m & =\sqrt{\left(d_u^0 \sin \phi_{u, 0}+m_z \Delta_R\right)^2+\left(l_{R, u}^m\right)^2}\\
& = \sqrt{\left(m_y \Delta_R\right)^2+\left(m_z \Delta_R\right)^2+\left(d_u^0\right)^2-2 d_u^0 m_y \Delta_R \cos \phi_{u, 0} \sin \theta_{u, 0}+2 m_z \Delta_R d_u^0 \sin \phi_{u, 0}}\\
& = d_u^0\sqrt{y^2+z^2+1-2 y \cos \phi_{u, 0} \sin \theta_{u, 0}+2 z \sin \phi_{u, 0}} \\
&\triangleq d_u^0 F(y, z)
\end{aligned}
\end{equation}
在远场条件下,可以直接利用一阶泰勒近似为
\begin{equation}
\begin{aligned}
d_{R, u}^m & \approx d_u^0\left(\left.F(y, z)\right|_{y=0, z=0}+\left.\frac{\partial F}{\partial y}\right|_{y=0}(y)+\left.\frac{\partial F}{\partial z}\right|_{z=0}(z)\right) \\
& =d_u^0\left(1-\cos \phi_{u, 0} \sin \theta_{u, 0} y+\sin \phi_{u, 0} z\right) \\
& =d_u^0\left(\frac{m_z \Delta_R}{d_u^0} \sin \phi_{u, 0}-\frac{m_y \Delta_R}{d_u^0} \sin \theta_{u, 0} \cos \phi_{u, 0}+1\right) \\
& =m_z \Delta_R \sin \phi_{u, 0}-m_y \Delta_R \sin \theta_{u, 0} \cos \phi_{u, 0}+d_u^0 .
\end{aligned}
\end{equation}
此时的阵列响应与普通的UPA阵列无异,其形式如下
\begin{equation}
\boldsymbol{a}_{R, u}^{F, i}\left(\omega_u, \varphi_u\right)[m]=\exp \left(-j \frac{2 \pi}{\lambda_i} J_m\left(\omega_u, \varphi_u\right)\right)
\end{equation}
其中$m$为两个方向分别的阵元index,$w$是到达阵列中心的虚拟角度(即$\sin\theta$或$\cos\theta$)。该公式为了方便表示,额外定义
\begin{equation}
J_m\left(\omega_u, \varphi_u\right)=m_z \Delta_R \omega_u-m_y \Delta_R \varphi_u
\end{equation}
在不同的角度定义中,该形式可以有各种不同的形式。只需要知道这是经典远场。
不同的是,由于菲涅尔近似时对相位要求的不同,这里采用比较常见的二阶近似,相关内容还可以参考我之前的微波全息入门。
\begin{equation}
\begin{aligned}
F(y, z) \approx &{} \left.F(y, z)\right|_{y=0, z=0}+\left.\frac{\partial F}{\partial y}\right|_{y=0} \times y+\left.\frac{\partial F}{\partial z}\right|_{z=0} \times z +\frac{1}{2}[y, z] \times \Delta^2 \boldsymbol{F} \times[y, z]^T\\
= &{} 1+\omega_u z-\varphi_u y+\frac{1}{2}\left(\bar{\omega}_u y^2+\bar{\varphi}_u z^2+2 \varphi_u \omega_u y z\right)
\end{aligned}
\end{equation}
with Hessian mat
\begin{equation}
\begin{aligned}
\Delta^2 \boldsymbol{F} & =\left[\begin{array}{cc}
\left.\frac{\partial^2 F}{\partial y^2}\right|_{y=0, z=0} & \left.\frac{\partial^2 F}{\partial z \partial y}\right|_{y=0, z=0} \\
\left.\frac{\partial^2 F}{\partial z \partial y}\right|_{y=0, z=0} & \left.\frac{\partial^2 F}{\partial z^2}\right|_{y=0, z=0}
\end{array}\right] \\
& =\left[\begin{array}{cc}
1-\left(\cos \phi_{u, 0} \sin \theta_{u, 0}\right)^2 & \cos \phi_{u, 0} \sin \theta_{u, 0} \sin \phi_{u, 0} \\
\cos \phi_{u, 0} \sin \theta_{u, 0} \sin \phi_{u, 0} & 1-\left(\sin \phi_{u, 0}\right)^2
\end{array}\right]
\end{aligned}
\end{equation}
其中$\bar{\omega}_u=1-\omega_u^2$, $\bar{\varphi}_u=1-\varphi_u^2$。此时我们可以将距离写成如下形式
\begin{equation}
\begin{aligned}
d_{R, u}^m \approx & m_z \Delta_R \omega_u-m_y \Delta_R \varphi_u+\frac{1}{2} \bar{\omega}_u \frac{\left(m_y \Delta_R\right)^2}{d_u^0} \\
& +\frac{1}{2} \bar{\varphi}_u \frac{\left(m_z \Delta_R\right)^2}{d_u^0}+\varphi_u \omega_u \frac{m_y \Delta_R\left(m_z \Delta_R\right)}{d_u^0}+d_u^0 \\
= & m_z \Delta_R \omega_u-m_y \Delta_R \varphi_u-\frac{\left(m_z \Delta_R \omega_u-m_y \Delta_R \varphi_u\right)^2}{2 d_u^0} \\
& +\frac{1}{2 d_u^0}\left(\left(m_z \Delta_R\right)^2+\left(m_y \Delta_R\right)^2\right)+d_u^0 \\
\triangleq & J_m\left(\omega_u, \varphi_u\right)+Q_m\left(\omega_u, \varphi_u, d_u^0\right)+d_u^0,
\end{aligned}
\end{equation}
这里出现的新定义$Q$实际上是由于二阶近似导致出现的二阶项,看起来与旁轴近似差不多。这样就可以写出近场模型
\begin{equation}
\begin{aligned}
\boldsymbol{a}_{R, u}^{N, i}\left(\omega_u, \varphi_u, d_u^0\right)[m]=\exp ( & -j \frac{2 \pi}{\lambda_i}\left(J_m\left(\omega_u, \varphi_u\right)\left.+Q_m\left(\omega_u, \varphi_u, d_u^0\right)\right)\right)
\end{aligned}
\end{equation}
不同的远近场模型均是为了参数估计等后续算法服务。
由于前面提到还有AP到RIS的链路,那么有$\boldsymbol{G}^i_{A, R}(m, n) = e^{j ({2 \pi}/{\lambda_i}) r_{m, n} }$, $\boldsymbol{H}^i_{A, R}=g_A^i \boldsymbol{G}^i_{A, R}$, 以及最终的级联信道
\begin{equation}\boldsymbol{h}_u^i=g_{u, i} \boldsymbol{G}_{A, R}^i \boldsymbol{E}_{R I S} \boldsymbol{a}_{u, i}\end{equation}
解决方案
RIS的训练相位采用DFT相位,此处不再介绍。训练帧结构是比较常见结构,不再赘述,观测模型为
\begin{equation}
\begin{aligned}
\boldsymbol{y}^i(t) & =\boldsymbol{G}_{A, R}^i \boldsymbol{E}_{R I S}(t) \sum_{u=1}^U g_u^i \boldsymbol{a}_{u, i} x_u(t)+\boldsymbol{n}_i(t) \\
& =\boldsymbol{G}_{A, R}^i \boldsymbol{E}_{R I S}(t) \boldsymbol{A}_i \boldsymbol{x}_t+\boldsymbol{n}_i(t)
\end{aligned}
\end{equation}
我们则需要从训练时收集的数据中估计出定位信息。
这里的观测很危险地暗示,观测阵列是全数字的。结合后面65天线观测140个大slot,我对此结果无话可说。目前我并不清楚ISAC算法是否都需要极大的导频数量,但是远超信道维度的观测数早就可以实现信道估计
为方便起见,将每个时刻的探测结果表示为
\begin{equation}\boldsymbol{y}_t=\boldsymbol{G}_{R I S} \boldsymbol{A} \boldsymbol{x}_t+\boldsymbol{n}_t\end{equation}
那么**显然**是可以通过LS估计到
\begin{equation}
\widehat{\boldsymbol{A x}}_t=\left(\boldsymbol{G}_{R I S}^H \boldsymbol{G}_{R I S}\right)^{-1} \boldsymbol{G}_{R I S}^H \boldsymbol{y}_t=\boldsymbol{H}_{R I S}^{\dagger} \boldsymbol{y}_t
\end{equation}
需要注意,如果想要实现不降秩的伪逆,我们需要$\boldsymbol{G}_{R I S}$是一个高阵。显然这里需要极高的观测数才能满足这个假设,否则会由于亏秩显著降低性能。一个可能的因素是,由于亏秩导致特征值较小,从而在inversion过程显著增加噪声的影响。
可以根据上述LS计算结果估计自相关矩阵为
\begin{equation}
\begin{aligned}
\tilde{\boldsymbol{R}} & =\mathbb{E}\left[\boldsymbol{H}_{R I S}^{\dagger} \boldsymbol{y}_t \boldsymbol{y}_t^H\left(\boldsymbol{H}_{R I S}^{\dagger}\right)^H\right] \\
& =\boldsymbol{A} \boldsymbol{A}^H+\sigma^2\left(\boldsymbol{G}_{R I S}^H \boldsymbol{G}_{R I S}\right)^{-1} .
\end{aligned}
\end{equation}
该结果还可以通过$\tau$个slot的观测估计
\begin{equation}
\hat{\boldsymbol{R}}=\frac{1}{\tau} \sum_{t=1}^\tau \widehat{\boldsymbol{A x}}_t\left(\widehat{\boldsymbol{A x}}_t\right)^H
\end{equation}
首先分析理想情况的性能,此时自相关矩阵满足
\begin{equation}
\boldsymbol{R}=\boldsymbol{A} \boldsymbol{A}^H=\sum_{u=1}^U\left|g_u\right|^2 \boldsymbol{a}_u \boldsymbol{a}_u^H
\end{equation}
其中第$(p,q)$位置的元素表示为
\begin{equation}
\boldsymbol{R}(p, q)=\sum_{u=1}^U\left|g_u\right|^2 \exp \left(-j \frac{2 \pi}{\lambda}\left(J_{p, q}+Q_{p, q}\right)\right)
\end{equation}
其中定义
\begin{equation}
\begin{aligned}
J_{p, q}&=J_p\left(\omega_u, \varphi_u\right)-J_q\left(\omega_u, \varphi_u\right)\\
&=\left(p_z-q_z\right) \Delta_R \omega_u-\left(p_y-q_y\right) \Delta_R \varphi_u
\end{aligned}
\end{equation}
和
\begin{equation}
\begin{aligned}
Q_{p,q}&=Q_p\left(\omega_u, \varphi_u, d_u^0\right)-Q_q\left(\omega_u, \varphi_u, d_u^0\right)\\
& =\frac{1}{2 d_u^0}\left(\Delta_R^2\left(p_z^2+p_y^2\right)\right)-\frac{1}{2 d_u^0}\left(p_z \Delta_R \omega_u-p_y \Delta_R \varphi_u\right)^2 \\& -\frac{1}{2 d_u^0}\left(\Delta_R^2\left(q_z^2+q_y^2\right)\right)+\frac{1}{2 d_u^0}\left(q_z \Delta_R \omega_u-q_y \Delta_R \varphi_u\right)^2
\end{aligned}
\end{equation}
方便表示,这两项的出现主要是自相关函数中对应位置的乘法导致。经过观察我们发现在一些特殊位置$p_z = -q_z$, $p_y=-q_y$中存在
\begin{equation}
J_{p, q}=2 p_z \Delta_R \omega_u-2 p_y \Delta_R \varphi_u, \quad Q_{p, q}=0
\end{equation}
即有
\begin{equation}
\begin{aligned}
\boldsymbol{R}\left(p\left(p_z, p_y\right)\right. & \left., q\left(-p_z,-p_y\right)\right) \\
& =\sum_{u=1}^U\left|g_u\right|^2 \exp \left(-j \frac{2 \pi}{\lambda}\left(2 J_p\left(\omega_u, \varphi_u\right)\right)\right)
\end{aligned}
\end{equation}
那么在这些特殊位置上的采样就可以作为合适的估计。首先我们定义对应位置的导引矢量为
\begin{equation}
\begin{aligned}
\boldsymbol{v}_u\left(\omega_u\right)[z]&=\exp \left(-j \frac{2 \pi}{\lambda}\left(2 z \Delta_R \omega_u\right)\right), z=0, \ldots, N_R^Z \\
\boldsymbol{s}_u\left(\varphi_u\right)[y]&=\exp \left(-j \frac{2 \pi}{\lambda}\left(-2 y \Delta_R \varphi_u\right)\right), y=0, \ldots, N_R^Y \\
\boldsymbol{b}_u\left(\omega_u, \varphi_u\right)&=\boldsymbol{v}_u\left(\omega_u\right) \otimes \boldsymbol{s}_u\left(\varphi_u\right)\\&=\left[\boldsymbol{v}_u\left(\omega_u\right)[0] \boldsymbol{s}_u^T\left(\varphi_u\right), \ldots, \boldsymbol{v}_u\left(\omega_u\right)\left[N_R^Z\right] \boldsymbol{s}_u^T\left(\varphi_u\right)\right]^T .
\end{aligned}
\end{equation}
值得注意的是这里导引矢量的spacing达到了初始导引矢量的两倍,因此为了后续操作能够正确区分角度,我们需要RIS的部署中以低于$\lambda/4$的spacing设计,或者约束服务范围。
经过巧妙的降采样设计,我们可以得到一个角度之间相互解耦的相关矩阵,因此可以通过MUSIC等算法实现角度估计
可惜最后还是需要brute-force search,类似MUSIC的谱搜索形式也在原文本小节最后给出,此处不再摘录。
近场的距离估计也是定位的重要内容。本文考虑的距离估计是建立在角度估计结束后的,这也意味着距离估计将放大角度估计误差的影响。此时阵列响应为
\begin{equation}
\boldsymbol{a}_R\left(\hat{\omega}_u, \hat{\varphi}_u, d_u^0\right)=\operatorname{diag}\left\{\boldsymbol{p}_u\left(\hat{\omega}_u, \hat{\varphi}_u\right)\right\} \boldsymbol{q}_u\left(\hat{\omega}_u, \hat{\varphi}_u, d_u^0\right),
\end{equation}
其中我们采用已经估计的角度定义了
\begin{equation}
\begin{aligned}
\boldsymbol{p}_u\left(\hat{\omega}_u, \hat{\varphi}_u\right)&=\left[\exp \left(-j \frac{2 \pi}{\lambda} J_{-N_0}\right), \ldots, \exp \left(-j \frac{2 \pi}{\lambda} J_{N_0}\right)\right]^T, \\
\boldsymbol{q}_u\left(\hat{\omega}_u, \hat{\varphi}_u, d_u^0\right)&=\left[\exp \left(-j \frac{\pi Q_{-N_0}}{\lambda d_u^0}\right), \ldots, \exp \left(-j \frac{\pi Q_{N_0}}{\lambda d_u^0}\right)\right] .
\end{aligned}
\end{equation}
利用这个导引矢量可以构建自相关矩阵,然后就是熟悉的MUSIC算法类似的方法计算距离。该方案需要提前知道用户的数量,以及距离的范围以实现brute-force search
最后是根据已经估计到的参数实现信道估计,最直接的方案就是least squares方案,透过
\begin{equation}
\begin{aligned}
\boldsymbol{y}_{t, i} & =\boldsymbol{G}_{R I S, i} \hat{\boldsymbol{A}}_i \operatorname{diag}\left(\boldsymbol{g}_i\right) \boldsymbol{x}_t+\boldsymbol{n}_t \\
& =\boldsymbol{G}_{R I S, i} \hat{\boldsymbol{A}}_i \operatorname{diag}\left(\boldsymbol{x}_t\right) \boldsymbol{g}_i+\boldsymbol{n}_t \\
& \triangleq \boldsymbol{G}_i \boldsymbol{g}_i+\boldsymbol{n}_t,
\end{aligned}
\end{equation}
我们计算
\begin{equation}
\boldsymbol{g}_i=\boldsymbol{G}_i^{\dagger} \boldsymbol{y}_{t, i}
\end{equation}
即可实现。其他细节例如直角坐标转换等问题详见论文Section III-D
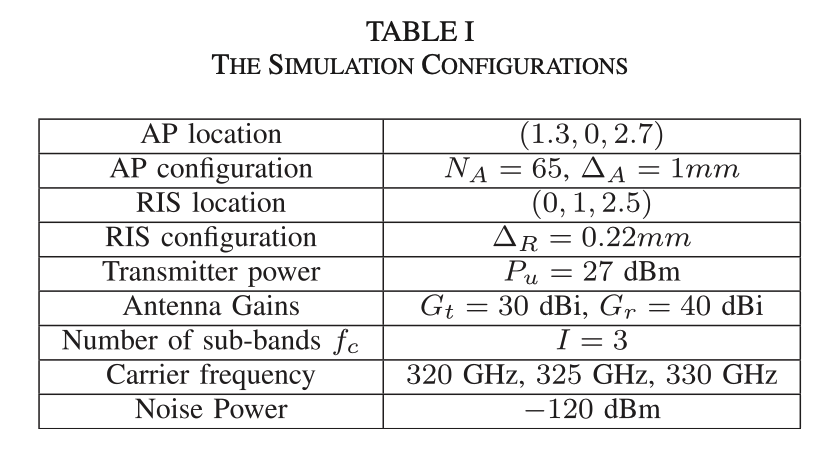
具体仿真结果不再额外展示,相关参数如下
小结
本文通过观察自相关矩阵的性质,提出了一种基于角度解耦的定位方法。然而,由于仍考虑基于MUSIC的方案,我们仍无法高效地定位(采样数多,计算复杂度高)。
扩展阅读
NULL