学习 feed

🔍 LMMSE一定比LS性能更好吗

📖 Textbook is All You Need

Posted by Shicong Liu on June 27, 2023

我的硕士生涯中未能认真学习很多课程，这直接导致了我基础知识匮乏。不过出乎我预料的是，大部分人在面对新问题时，都很难充分利用自己已经学到的知识——这让我们在实际问题中没有产生较大的差异。

LS 与 LMMSE 方法回顾

这个问题本身是个很无聊的问题。LS方法和LMMSE方法针对的优化目标不同，因此在不同准则下最优，不过在许多场景中MMSE的目标函数都会更契合现实问题，因此性能也会更为突出。那么今天的问题最初(对于我来说)来自于2023-03-21日万老师发起的讨论，如图

Q

该问题出自当时预定于4月4日组会要讨论的论文《Orthogonal Chirp Division Multiplexing》1，该文章主要介绍了一种采用正交Chirp函数族作为基函数的复用调制技术，与OFDM的不同点在于采用正交菲涅尔变换替代了傅立叶变换。本文的第9页左侧Section VI-B部分提到仿真中的检测方法为迫零(Zero Forcing, ZF)，而非最小均方误差(Minimum Mean Square Error, MMSE)检测器，其原因是二者性能相同。

这里与常识冲突的问题为，ZF方法在绝大多数场景中都没有MMSE(甚至线性MMSE, 即LMMSE)方法效果好，这里提出的性能相同并不符合惯性常识。我们可以简单分析一下这个问题，对$K$载波的OFDM系统中，每一个时隙中的传输模型可以描述为

$$ \begin{equation} {\bf y} = {\bf H}{\bf x}+{\bf n}\label{q1} \end{equation} $$

其中${\bf H}\in\mathbb{C}^{K\times K} = {\rm diag}([{\bf h}_1,\dots,{\bf h}_K])$是对角的信道矩阵，${\bf x}\in\mathbb{C}^K$和${\bf y}\in\mathbb{C}^K$分别为发送和接收符号矢量，${\bf n}\in\mathbb{C}^K$则是噪声矢量。LS和LMMSE线性检测器${\bf W}$的处理如下

$$ \begin{equation} \begin{aligned} {\bf z}_{\rm LS} & = {\bf W}_{\rm LS}{\bf y} = {\bf W}_{\rm LS}\left( {\bf H}{\bf x}+{\bf n} \right)\\ & = {\bf x} + \left( {\bf H}^{\rm H}{\bf H} \right)^{-1}{\bf H}^{\rm H}{\bf n} \end{aligned} \end{equation} $$
$$ \begin{equation} \begin{aligned} {\bf z}_{\rm LMMSE} & = {\bf W}_{\rm LMMSE}{\bf y} = {\bf W}_{\rm LMMSE}\left( {\bf H}{\bf x}+{\bf n} \right)\\ & = \left( {\bf H}^{\rm H}{\bf H} +\frac{\sigma_n^2}{\sigma_s^2} \right)^{-1}{\bf H}^{\rm H}{\bf H}{\bf x} + \left( {\bf H}^{\rm H}{\bf H} +\frac{\sigma_n^2}{\sigma_s^2} \right)^{-1}{\bf H}^{\rm H}{\bf n} \end{aligned} \end{equation} $$

$\blacksquare\quad$Least Squares

在上述观测问题$\eqref{q1}$中，Least Squares方法对${\bf x}$的估计是最小化误差

$$ \begin{equation} \underset{ \hat{\bf x} }{ {\min} }\ \left\Vert {\bf y}-{\bf H}\hat{\bf x} \right\Vert \end{equation} $$

简单地说，最小化该误差的方法就是寻找First Order Condition

$$ \begin{equation} \frac{\partial}{\partial \hat{\bf x} }\left[\|{\bf y}-{\bf H} \hat{\bf x}\|^2\right]=\frac{\partial}{\partial \hat{\bf x} }\left[({\bf y}-{\bf H} \hat{\bf x})^{\rm H}({\bf y}-{\bf H} \hat{\bf x})\right] = 0 \end{equation} $$

上式写成标量的形式就是

$$ \begin{equation} \frac{\partial}{\partial {\bf x} }\left[\sum_{i=1}^K\left({\bf y}_i-({\bf H} \hat{\bf x})_i\right)\left({\bf y}_i-({\bf H} \hat{\bf x})_i\right)^*\right] \end{equation} $$

将其中的$({\bf H}\hat{\bf x})_i$作为偏微分的中间变量，容易求得

$$ \begin{equation} \frac{\partial}{\partial \hat{\bf x} }\left[\|{\bf y}-{\bf H} \hat{\bf x}\|^2\right] = \sum_{i=1}^K-2\left({\bf y}_i-({\bf H} \hat{\bf x})_i\right)^* {\bf H} = -2{\bf H}^{\rm H} ({\bf y}-{\bf H}\hat{\bf x}) = 0 \end{equation} $$

那么很显然LS解就是(前提是逆矩阵存在)

$$ \begin{equation} \begin{aligned} \hat{\bf x} & = \left({\bf H}{\bf H}^{\rm H}\right)^{-1} {\bf H}^{\rm H}{\bf y}\\ & = {\bf x}+\left({\bf H}{\bf H}^{\rm H}\right)^{-1} {\bf H}^{\rm H}{\bf n} \end{aligned} \end{equation} $$

此时LS检测器${\bf W}_{\rm LS} = \left({\bf H}{\bf H}^{\rm H}\right)^{-1} {\bf H}^{\rm H}$

$\blacksquare\quad$Minimum Mean Square Error

与此相反，MMSE的思路，直观上是最小化估计结果与真实值之间的「距离」

$$ \begin{equation} \underset{ \hat{\bf x} }{ {\min} }\ \left\Vert {\bf x}-\hat{\bf x} \right\Vert \label{mmse} \end{equation} $$

不过很显然我们对待估计量${\bf x}$是没有全部知识的。当我们使用MSE这个term的时候，我们实际上已经将目标与贝叶斯准则联系起来。对于目标${\rm MSE}(\hat{\bf x}) = {\mathbb{E}}\left[ ({\bf x}-\hat{\bf x})^2 \right]$，我们可以将其写作

$$ \begin{equation} \begin{aligned} {\rm MSE}(\hat{\bf x}) &= \iint \left({\bf x}-\hat{\bf x}\right)^2 p({\bf x},{\bf y}){\rm d}{\bf x}{\rm d}{\bf y}\\ &=\int \left[ \int \left({\bf x}-\hat{\bf x}\right)^2 p({\bf x}\mid {\bf y}){\rm d}{\bf x} \right] p({\bf y}){\rm d}{\bf y} \end{aligned} \end{equation} $$

最小化MSE，我们还可以继续计算First Order Condition

$$ \begin{equation} \begin{aligned} \frac{\partial}{\partial \hat{\bf x}} \int \left({\bf x}-\hat{\bf x}\right)^2 p({\bf x}\mid {\bf y}){\rm d}{\bf x} &= \int \frac{\partial}{\partial \hat{\bf x}} \left({\bf x}-\hat{\bf x}\right)^2 p({\bf x}\mid {\bf y}){\rm d}{\bf x} \\ & = \int -2 \left({\bf x}-\hat{\bf x}\right) p({\bf x}\mid {\bf y}){\rm d}{\bf x} \\ & = -2 \int {\bf x} p({\bf x}\mid {\bf y}){\rm d}{\bf x} +2 \int \hat{\bf x} p({\bf x}\mid {\bf y}){\rm d}{\bf x}\\ & = 0, \end{aligned} \end{equation} $$

容易知道

$$ \begin{equation} {\rm MSE}(\hat{\bf x}) = \int {\bf x} p({\bf x}\mid {\bf y}){\rm d}{\bf x} = \mathbb{E}\left[ {\bf x}\mid {\bf y} \right] \end{equation} $$

即MSE就是后验均值。在绝大多数场景中后验均值均不能通过简单的方案获得2，因此线性MMSE在大部分此类场景中使用。我们假设线性检测器是${\bf W}_{\rm MMSE}$，此时MSE可以表示为

$$ \begin{equation} {\rm MSE}(\hat{\bf x}) = \mathbb{E}\left[ \left\Vert {\bf x}-\hat{\bf x} \right\Vert_2^2 \right] = \mathbb{E}\left[ \left( {\bf x}-\hat{\bf x} \right)^{\rm H} \left( {\bf x}-\hat{\bf x} \right) \right] = \mathbb{E}\left[ {\rm tr}\left( \left( {\bf x}-\hat{\bf x} \right) \left( {\bf x}-\hat{\bf x} \right)^{\rm H} \right) \right] \end{equation} $$

此时的检测结果$\hat{\bf x} = {\bf W}_{\rm MMSE}{\bf y}$满足公式$\eqref{mmse}$的优化目标，则最小化条件

$$ \begin{equation} \begin{aligned} \frac{\partial}{\partial {\bf W}_{\rm MMSE}} {\rm MSE} (\hat{\bf x}) &= \frac{\partial}{\partial {\bf W}_{\rm MMSE}} {\rm tr} \left( {\mathbb E}\left[ {\bf x}{\bf x}^{\rm H} \right] - {\bf W}_{\rm MMSE}{\mathbb E}\left[ {\bf y}{\bf x}^{\rm H} \right] - {\mathbb E}\left[ {\bf x}{\bf y}^{\rm H} \right]{\bf W}_{\rm MMSE}^{\rm H} \right)\\ & = -2{\mathbb E}\left[ {\bf y}{\bf x}^{\rm H} \right]+2{\mathbb E}\left[ {\bf y}{\bf y}^{\rm H} \right]\\ & = 0, \end{aligned} \end{equation} $$

容易计算

$$ \begin{equation} \hat{\bf x} = \left( {\mathbb E}\left[ {\bf y}{\bf y}^{\rm H} \right] \right)^{-1} {\mathbb E}\left[ {\bf y}{\bf x}^{\rm H} \right] \overset{(a)}{=} \left( {\bf H}{\bf H}^{\rm H} + \frac{\sigma_n^2}{\sigma_x^2} \right)^{-1}{\bf H}, \end{equation} $$

其中$(a)$条件假设$\bf x$和$\bf y$是联合i.i.d.高斯、均值为$0$等。值得一提的是，当问题符合上述条件时，MMSE与LMMSE等价。

这个问题十分简单，EE专业的硕士生(甚至于能力较强的本科生)都能比较轻易地理解并推导。由于LMMSE针对的目标直观上有着更高的普适性(估计符号与原符号之间的距离)，因此在绝大部分问题中都获得了更好的性能。那么回到最初的问题，在检测问题上ZF(实际上就是LS)和LMMSE真的有相同的性能表现吗？解决此类问题我的风格一般是先仿真后分析，我们简单搭建一个MATLAB仿真环境如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

clear all
close all
%% MPSK
mod_order = 2;
M = 2^mod_order;
Nframe = 400;
Nslot = 50;
Nfft = 1024;
Nchannel = Nfft;
Nbits = Nframe*Nslot*Nfft*mod_order;
bits = randi([0 1],[Nframe,Nslot,Nfft*mod_order]);
pskmod_ = comm.PSKModulator(ModulationOrder=M,PhaseOffset=pi/M,BitInput=true,SymbolMapping="Gray");
pskdemod_ = comm.PSKDemodulator(ModulationOrder=M,PhaseOffset=pi/M,BitOutput=true,SymbolMapping="Gray");
snr_list = -5:2:20;
ber_zf = zeros(numel(snr_list),1);
ber_lmmse = zeros(numel(snr_list),1);
tic
for n = 1:numel(snr_list)
    snr = 10^(snr_list(n)/10);
    bit_err_zf = 0;
    bit_err_lmmse = 0;
    for frame = 1:Nframe
        h = (randn(Nchannel,1)+1j*randn(Nchannel,1))/sqrt(2);
        h_f = fft(h,Nfft)/sqrt(Nfft);
        for slot = 1:Nslot
            curr_bits = squeeze(bits(frame,slot,:));
            txSig = pskmod_(curr_bits);
            txSymbol = ifft(txSig)*sqrt(Nfft);
            rxSignal = ifft((fft(txSymbol)/sqrt(Nfft)).*(fft(h,Nfft)/sqrt(Nfft)))*sqrt(Nfft);
            s = norm(rxSignal)^2;
            sigma = sqrt(s/snr);
            rxSymbol = rxSignal + sigma.*(randn(Nfft,1)+1j*randn(Nfft,1))/sqrt(2)/sqrt(Nfft);
            % eq
            rxSymbol_zfeq = (fft(rxSymbol)/sqrt(Nfft)).*(conj(h_f)./(h_f.*conj(h_f)+0.*ones(Nfft,1)));
            rxSymbol_lmmseeq = (fft(rxSymbol)/sqrt(Nfft)).*(conj(h_f)./(h_f.*conj(h_f)+((sigma^2)/s).*ones(Nfft,1)));
            demod_zf = pskdemod_(rxSymbol_zfeq);
            demod_lmmse = pskdemod_(rxSymbol_lmmseeq);
            bit_err_zf = bit_err_zf + biterr(curr_bits,demod_zf);
            bit_err_lmmse = bit_err_lmmse + biterr(curr_bits,demod_lmmse);
        end
    end
    ber_zf(n) = bit_err_zf/Nbits;
    ber_lmmse(n) = bit_err_lmmse/Nbits;
end
toc
%%
figure
semilogy(snr_list-10*log10(mod_order),ber_zf,'-o',MarkerSize=10,LineWidth=1.75);
hold on
semilogy(snr_list-10*log10(mod_order),ber_lmmse,'-s',MarkerSize=10,LineWidth=1.75);
grid on
legend('ZF','LMMSE')
xlabel('Eb/N0')
ylabel('BER')
set(gca,'fontsize',14);

该仿真考虑在PSK符号映射的条件下进行OFDM传输，假设接收端对Rayleigh信道$\bf H\sim {\mathcal{CN}({\bf 0},\sigma^2{\bf I})}$完美已知，分别采用LS和LMMSE方法进行符号检测。判决器为硬阈值判决，理论值通过MATLAB bertool工具包计算，均假设为AWGN噪声环境。仿真结果如图，实际上LS方法和LMMSE方法在数值上性能完全一致，并均能与理论界吻合。

PSK

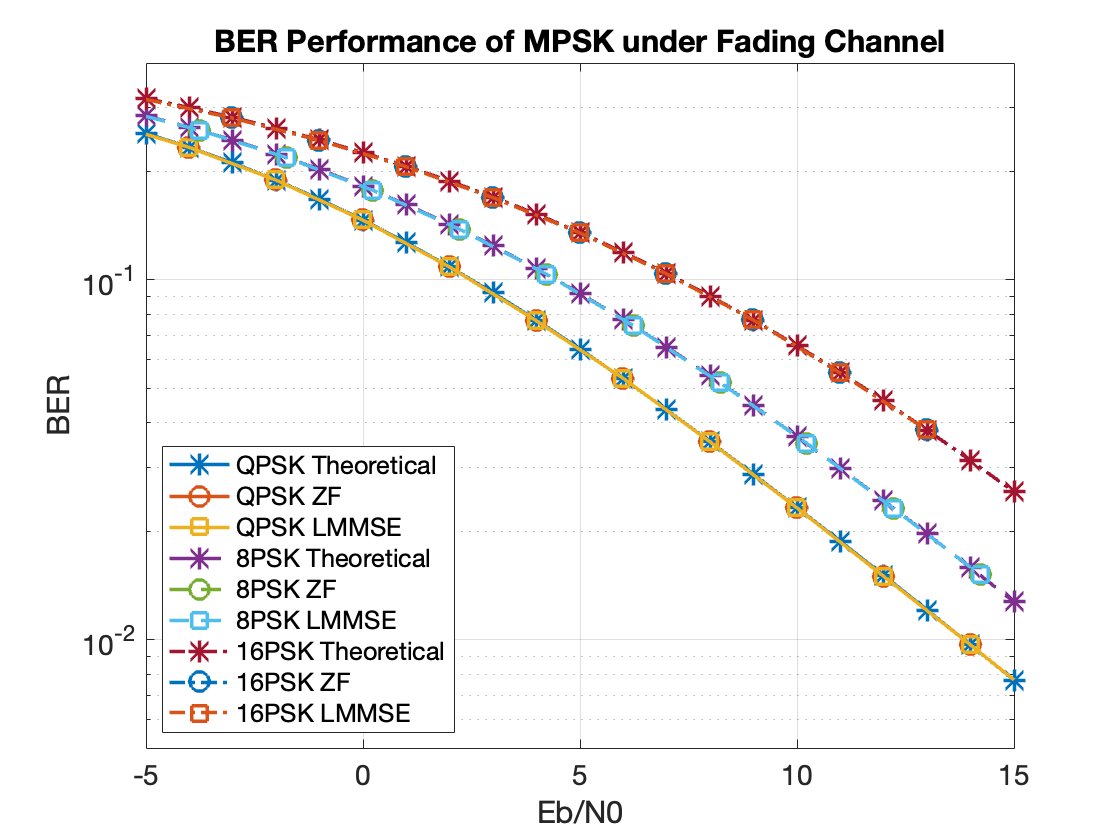
出现上述性能的原因不难分析，由于PSK调制方法的判决界为过零点直线，因此均衡后符号的幅值并不会影响检测结果。而在OFDM系统中，信道可以视作对角信道，此时的LS与LMMSE方法的唯一差异即为分母上的噪声功率产生的幅度差，并不影响结果。PSK调制的仿真更像是一种「特殊情况」，如果考虑更为普适的QAM调制，类似的问题就不会出现。代码只需要较少改动，结果如下

不知为何MATLAB的8-QAM解调效率非常低，大约是其他QAM速度的$1/6$

QAM

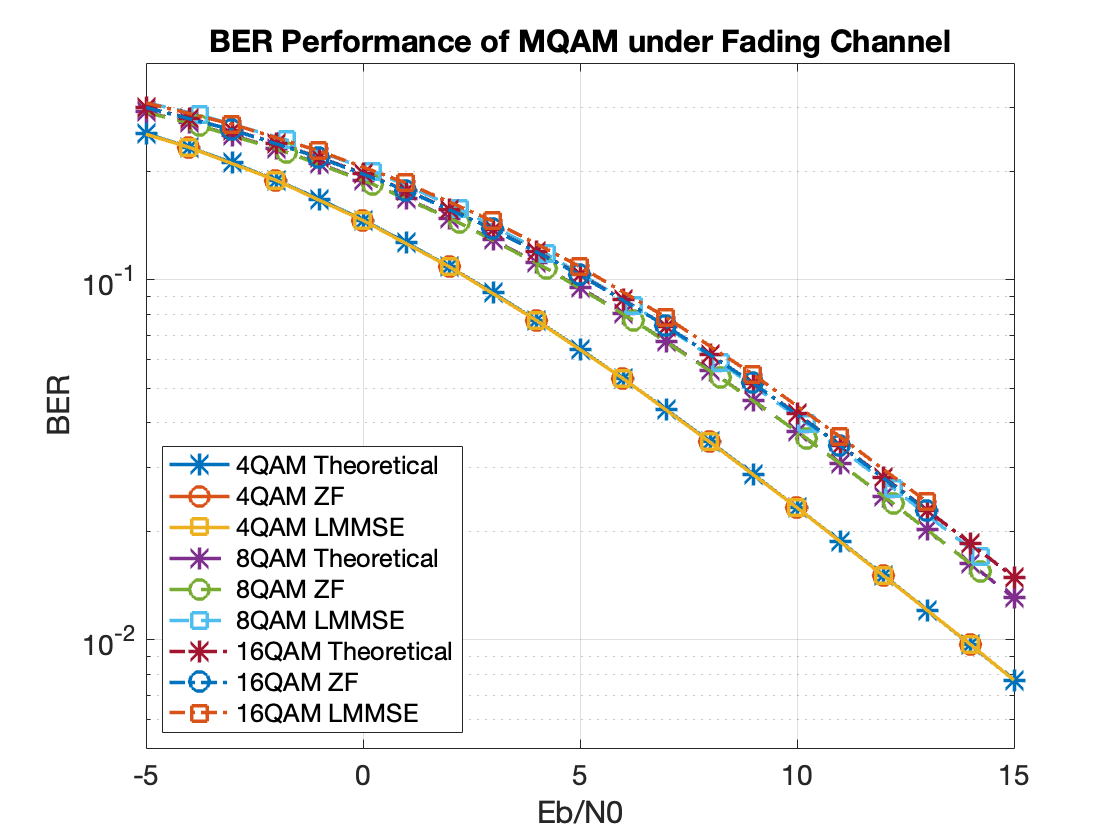
由于4QAM于QPSK基本等价因此没有性能差异，其他阶数QAM调制的条件下我们均可以观测到LS与LMMSE性能的不同，而反直觉的是，均为LS性能更好，与理论界相符。以16QAM为例，在$10$dB的$E_b/N_0$条件下(效果更明显)观测星座图可以得到

QAM

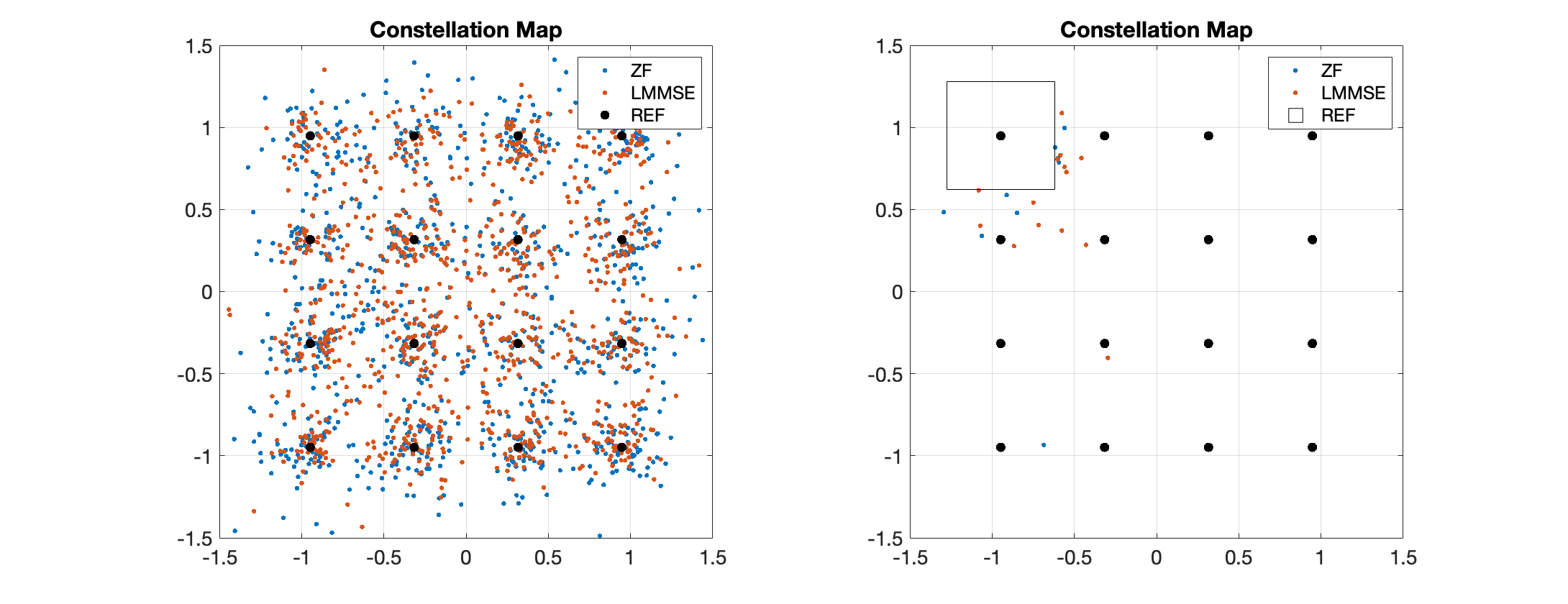
由于LMMSE检测器本身的特点，其检测结果的幅度小于LS。而LS方案是无偏估计，LMMSE方案渐进无偏，在单次实现中我们容易发现LMMSE的误码可能更高。同一次实现中，我们选取左上角星座点作为参考点，粗略绘制出其判决界(实际上左、上方全部区域均为该点的判决域，这里只是示意图)，可以看出LS方案只有$10$个点错判，而LMMSE方案则出现了$14$个误码点。

该图片并没有展示出来的是，部分LS方案的错点在图框之外，部分星座点检测结果幅度甚至大于了$10$。这可以通过LS方案增强噪声来简单理解，而通过最小化距离准则检测的方法确实实现了最小距离(但代价是有偏估计带来的BER损失)，仿真计算结果如下表所示。

附表：LS 和 LMMSE方法在10dB下的LS与MSE损失函数仿真结果
  LS LMMSE
LS Loss $\bf 63.099$ $72.223$
MSE Loss $1672.422$ $\bf 206.821$

LS估计的偏差为

$$ \begin{equation} \begin{aligned} {\mathbb{E} }\left[ \hat{\bf x}-{\bf x} \right] &= {\mathbb{E}}\left[ \left({\bf H}{\bf H}^{\rm H}\right)^{-1} {\bf H}^{\rm H} {\bf y} - {\bf x} \right]\\ &= {\mathbb{E}}\left[ \left({\bf H}{\bf H}^{\rm H}\right)^{-1} {\bf H}^{\rm H} ({\bf Hx+n}) - {\bf x} \right]\\ & = {\mathbb{E}}\left[ \left({\bf H}{\bf H}^{\rm H}\right)^{-1} {\bf H}^{\rm H} {\bf n} \right]\\ & = 0, \end{aligned} \end{equation} $$

是无偏估计，而LMMSE则显然为

$$ \begin{equation} \begin{aligned} {\mathbb{E} }\left[ \hat{\bf x}-{\bf x} \right] &= {\mathbb{E}}\left[ \left({\bf H}{\bf H}^{\rm H} +\frac{\sigma_n^2}{\sigma_s^2}{\bf I} \right)^{-1} {\bf H}^{\rm H} {\bf y} - {\bf x} \right]\\ &= {\mathbb{E}}\left[ \left({\bf H}{\bf H}^{\rm H} +\frac{\sigma_n^2}{\sigma_s^2}{\bf I} \right)^{-1} {\bf H}^{\rm H} ({\bf Hx+n}) - {\bf x} \right]\\ & = {\mathbb{E}}\left[ \left(\left({\bf H}{\bf H}^{\rm H} +\frac{\sigma_n^2}{\sigma_s^2}{\bf I} \right)^{-1} {\bf H}^{\rm H} {\bf H}-{\bf I}\right){\bf x} \right]\\ & \neq 0, \end{aligned} \end{equation} $$

其有偏性恰恰成为了BER问题中的缺陷。容易发现随着$\bf x$的增加，其偏差也会随之增大，在仿真中我们也同时观测到了内圈星座点误码率LMMSE更低，而外圈误码率LMMSE远高于LS的情况。

值得一提的是该问题的讨论在我们课题组中已经扩大化到了其他层面，后续我们继续跟进更新细节~

扩展阅读

  1. X. Ouyang and J. Zhao, “Orthogonal Chirp Division Multiplexing,” in IEEE Transactions on Communications, vol. 64, no. 9, pp. 3946-3957, Sept. 2016, doi: 10.1109/TCOMM.2016.2594792. ↩

  2. [Wikipedia] Minimum Mean Square Error ↩

CATALOG
    FEATURED TAGS
    学习 feed 摸鱼 日常 生活