TWC’25 补充说明
Comments and Discussions for TWC’25

7 minutes read

Published: January 02, 2026

Translation Provider: Google

首先感谢各位审稿人和编辑的宝贵意见，以及一轮不杀之恩。本文目前仍在Major Revision阶段，arXiv版本目前已经可以查看。二轮审稿时间略长，目前未出结果，正赶上元旦假期闲来无事，随便写写这篇手稿的补充说明，万一真有人看呢。如果本稿件有机会被接受发表，我会comment一些其他内容进来。

由于本文的研究内容个人感觉还算有趣，且尝试使用了一些不太常见的数学工具，所以我想顺手记录一下本文撰写过程中的一些想法。

Motivation

K.-K. Wong老师很早的时候就在全球通信圈中推广fluid antenna这一概念。在2021年前后我还在读硕士期间，Wong老师就受邀在北理工高镇教授课题组进行过相关讲座。当时的引言还是经典的Bruce Lee，我的印象中当时的讲座更倾向于理论上的分析和论证。由于我不是天线专业，当时其实没有太关注这个方向，纯感觉十分fancy。

后来Movable概念也出现，我才逐渐感受到天线位置的改变会对通信性能产生一定的影响。不过早期的研究还是聚焦于少量天线的位置优化，这是因为当时提出的一些算法在天线数量增加时会受到急剧扩张的解空间、高次多项式的优化复杂度、非线性约束等各种因素影响。

由于入门时就接触massive MIMO（路径依赖说是），所以我的第一感觉还是想做天线更多的场景。但是既然常规优化算法不太好做，我只能尝试另辟蹊径。

对于天线较多的场景，我首先和以前一样¹考虑了空间自相关函数:

$$ {\bf K}_f[n,n^\prime]= \frac{1}{M} \sum_{m=1}^{M} h\left({\bf r}_{\rm R}^{(n)},{\bf r}_{\rm T}^{(m)}\right)h^*\!\left({\bf r}_{\rm R}^{(n^\prime)},{\bf r}_{\rm T}^{(m)}\right). \label{eq:gram1} $$

因为我们假设了天线数量足够大，那么这个求和可以表示为黎曼积分:

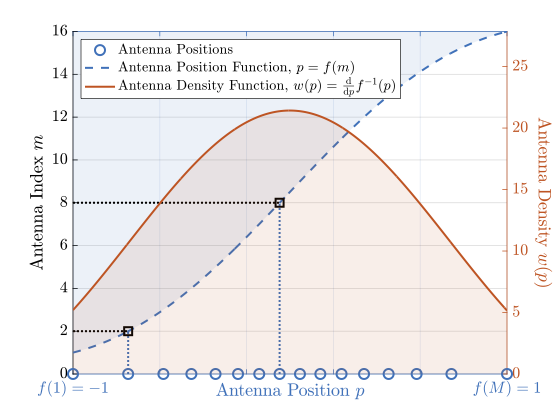
$$ \tilde{\bf K}_f[n,n^\prime] = \int_{1}^{M} h\left({\bf r}_{\rm R}^{(n)},{\bf r}_{\rm T}^{(m)}\right)h^*\left({\bf r}_{\rm R}^{(n^\prime)},{\bf r}_{\rm T}^{(m)}\right)\,{\rm d}m.\label{eq:gram2} $$

如果我们假设每个天线的位置可以通过索引 $m$ 的函数来描述，即 $p = f(m)$，其中 $f(m)$ 是个严格单调增函数，那么通过 $m=f^{-1}(p)$我们得到

$$ \begin{align} \tilde{\bf K}_f[n,n^\prime] ={}&\int_{-1}^{1} h\left({\bf r}_{\rm R}^{(n)},\tilde{\bf r}_{ {\rm T} }^{(p)}\right) h^*\left({\bf r}_{\rm R}^{(n^\prime)},\tilde{\bf r}_{ {\rm T} }^{(p)}\right)\frac{\rm d}{ {\rm d} p} {f}^{-1}(p)\,{\rm d}p\notag\\ ={}&\int_{-1}^{1} w(p)h\left({\bf r}_{\rm R}^{(n)},\tilde{\bf r}_{ {\rm T} }^{(p)} \right) h^*\left({\bf r}_{\rm R}^{(n^\prime)},\tilde{\bf r}_{ {\rm T} }^{(p)} \right)\,{\rm d}p\notag\\ \triangleq{}&\tilde{\bf K}_w[n,n^\prime],\label{eq:kernel_p} \end{align} $$

其中 $w(p) = \frac{\rm d}{ {\rm d} p} {f}^{-1}(p)$ 代表了单位长度下天线的数量，因此是天线位置的密度函数。

天线位置和密度函数对照

计算最佳密度

通过上述过程我们很自然能想到，如果能找到最佳密度函数，我们也能实现最大化频谱效率。想要获得一个最优函数，我们就需要使用泛函工具。不过泛函直接分析在这个问题上还是太复杂了，所以我们主要采用了两种方案来处理

数值优化

简单地说，我们将这个函数视作一个P格点的矢量，其中格点数大于天线数量，即$P>M$。然后通过计算梯度，我们构造了一个基于梯度投影的优化算法。在近场场景下，我们能够得到如下的密度函数估计

数值优化的密度函数

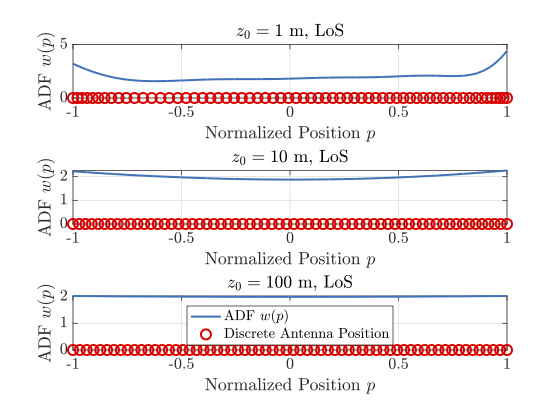
可以看到，最佳密度函数在边缘处有明显的峰值，这和我们后续通过Szego定理得到的结论是一致的。

（扩展的）Szego定理分析

由于空间自相关矩阵，本文称为Gram矩阵，本质上是Toeplitz矩阵，在天线数量足够大的情况下，我们可以利用Szego定理来渐近分析其特征谱。

在一些比较合理的近场建模下，我们可以将Gram矩阵的行/列元素表示为天线密度函数的截断傅里叶变换:

$$ \begin{align} \overline{\bf K}_{f}\left[n,n^\prime\right] &=\frac{1}{z_0^2}\int_{1}^{M} \frac{e^{-\jmath\beta {\Delta n} p} }{\left( 1+ \tau p \right)^2 }\,{\rm d} f^{-1}(p)\label{eq:nflos_kernel}\\ &=\frac{1}{z_0^2}\int_{-1}^{1} \frac{w(p)}{\left( 1+ \tau p \right)^2} e^{-\jmath\beta {\Delta n} p }\,{\rm d} p\triangleq \overline{\bf K}_w\left[n,n^\prime\right]. \end{align} $$

其中

$$ \begin{equation} \tilde{w}(p) = \frac{w(p)}{\left( 1+ \tau p \right)^2}, \end{equation} $$

是加权后的天线密度函数。这个函数同时是这个Toeplitz矩阵的生成函数（符号函数），其性质决定了Gram矩阵的特征谱。简单地说，我们有如下定理

Theorem 1 (Fisher-Hartwig Conjecture)²: 对于定义在单位圆上的实生成函数 $s(\theta)$，若其存在$R$个奇异点$\theta_r$，且满足如下形式:
$$ s(\theta)= b(\theta)\prod_{r=1}^{R} \left|2-2\cos\left(\theta-\theta_r \right) \right|^{\alpha_r}, $$
其中$b(\theta)$是严格正的光滑函数，且$\alpha_r > -\frac{1}{2}$。由该函数生成的Toeplitz矩阵$\bf T$满足如下渐近性质:
$$ \begin{align} &\lim_{N\to \infty} \log \det \left( {\bf T}_N \right)\\ ={}& E_b\left(\theta\right) + \log N\sum_{r=1}^{R} \alpha_r^2 +\sum_{r=1}^{R} \frac{ {\rm BG}^2(1+\alpha_r)}{ {\rm BG}(1+2\alpha_r)}\\ &+\sum_{1\leq r<s\leq R} \left\vert2-2\cos\left(\theta_r-\theta_s \right) \right\vert^{-\alpha_r\alpha_s} + {\mathcal O}(1), \end{align} $$
其中
$$ \begin{equation} E_b\left(\theta\right) =\frac{N}{2\pi} \int_{-\pi}^{\pi}\log b(\theta)\,{\rm d}\theta + E_0, \label{eq:eb} \end{equation} $$
$$ \begin{equation} E_0 = \sum_{k=1}^{\infty} k \left( \log b(\theta) \right)_k \left( \log b(\theta) \right)_{-k}<\infty, \label{eq:condszego} \end{equation} $$
且 ${\rm BG}(\cdot)$ 是Barnes-G函数，$\left(\log b(\theta) \right)_k$ 是 $b(\theta)$ 的傅里叶系数。

从物理可行性上分析，我们认为奇异点应只存在于边缘处，且奇异程度越高，带来的频谱效率增益越强（详见原文）。对于$\alpha = 0$的情况，最优的密度函数应为

$$ \begin{equation} w(p;\alpha=0) \triangleq \frac{3\left( M-1 \right)}{6+2\tau^2} \left( 1+\tau p \right)^2. \end{equation} $$

对于$-1/2<\alpha < 0$的情况，最优密度函数应为

$$ \begin{equation} w(p;-0.5\!<\!\alpha\!<\!0) \triangleq \left( \frac{\gamma_\alpha}{\left( 1 - p^2 \right)^{-2\alpha}} \!-\! \frac{\beta z_0^2}{2\pi\rho} \right) (1+\tau p)^2, \label{eq:optadf} \end{equation} $$

其中 $\gamma_\alpha$ 是归一化系数。

从密度函数到离散天线位置

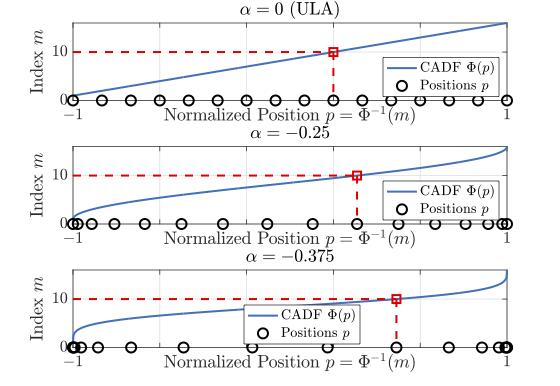
由于最终需要部署离散天线，我们需要将密度函数转化为具体的天线位置。本文采用了一种简单的累计分布函数反演的方法:

$$ \begin{equation} \Phi\left( p \right) = \int_{-1}^{p} {w}(p)\,{\rm d}p. \label{eq:cadf} \end{equation} $$

$$ \begin{equation} p = f(m) = \Phi^{-1}(m). \label{eq:cdfmethod0} \end{equation} $$

对于massive MIMO且距离不极端近的场景，我们还有闭式解

$$ \begin{equation} \begin{aligned} p &= \Phi^{-1}(m) = f(m)\\ &=\sqrt{B^{-1}\left(\frac{2m-\left(M+1\right)}{\gamma_\alpha};\frac{1}{2},1+2\alpha\right)}, \end{aligned} \label{eq:cdfmethod} \end{equation} $$

其中 $B^{-1}(\cdot)$ 是不完全Beta函数的反函数。值得注意的是这是一种很常见很直观的离散化方法，也十分有利于渐近分析。采用该方法进行量化时，在没有额外的物理约束情况下（例如天线间距限制），我们可以证明，随着天线数量趋近于无穷大，离散天线位置部署方案的性能将会收敛到理论最优密度函数。

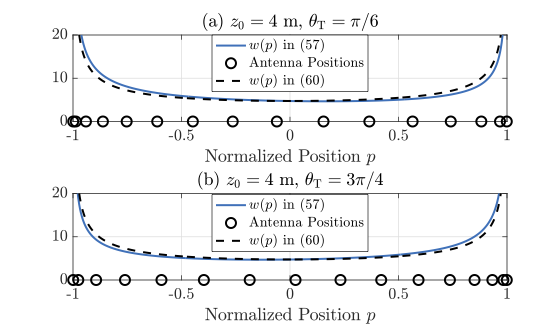
下面是一些密度函数结果展示

不同$\alpha$下的密度函数和离散天线位置

不同用户位置下的最优密度与位置

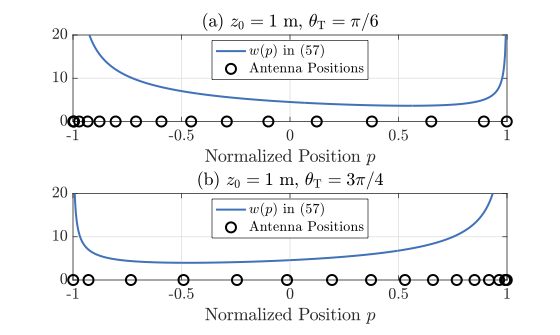引用格式

如果您觉得本文对您的研究有所帮助，欢迎引用:

@misc{liu2025nf_mma,
	title={Near-Field Communication with Massive Movable Antennas: {A} Functional Perspective}, 
	author={Shicong Liu and Xianghao Yu and Jie Xu and Rui Zhang},
	year={2025},
	eprint={2508.01201},
	archivePrefix={arXiv},
	primaryClass={cs.IT},
	url={https://arxiv.org/abs/2508.01201}, 
}

S. Liu, X. Yu, J. Xu, and R. Zhang, ``Near-Field Communication with Massive Movable Antennas: A Functional Perspective,'', 2025. [Online]. Available: https://arxiv.org/abs/2508.01201

如有兴趣，也敬请关注后续论文。

~~更多内容待续~~

~~To Be Continued~~

拓展阅读

Share on

Twitter Facebook LinkedIn

Shicong LIU