Translation Provider: Google
今日我们的一篇基于离散长球变换的近场信道估计的论文被Flagship会议ICC’24正会的Wireless Communications Symposium接收,pre-print目前可以在arXiv上阅读。本文简单介绍提出方案的思路,并对部分审稿人意见的予以解答。
背景
近年来,受到RIS等超大规模阵列的影响,通信的研究方向逐渐向光学靠近,因此一些球面波假设、衍射现象等被许多论文反复提及。近场条件下,即使是视距信道也能调制多流传输,这是由于近场信道条件下的信道建模方式改变,这增大了信道矩阵的秩,但也导致传统的压缩感知方法需要更多的导频实现精确信道估计。
目前已经有不少研究者考虑到了稀疏化字典的影响,并设计了极坐标码本、chirp码本、分层码本,甚至采用了码本学习的方法为特定场景单独设计字典的方案。这些方案目前而言都存在缺陷,例如极坐标码本、chirp的多个自由度会导致很高的字典容量、非正交码字,码本学习的计算量则较高。我们希望提出一种计算量比较低,码字相互正交,性能更好的字典,从而降低近场信道估计的复杂度。
系统模型
假设近场位置的用户阵列与基站通信,则此时在用户终端上产生的电场 \({\bf E}\)可以用格林函数与基站电流源 \({\bf J}\) 表示
\begin{equation} {\bf E}({\bf r}_{\rm R}) = \int_{ {\mathcal{S}_{\rm T} } } {\mathbf{G} }\left({\bf r}_{\rm T},{\bf r}_{\rm R}\right) {\bf J}({\bf r}_{\rm T})~{\rm d}{\bf r}_{\rm T}, \end{equation}
其中格林函数有如下形式
\begin{align} {\mathbf{G}}\left({\bf r}_{\rm T},{\bf r}_{\rm R}\right) = {} & {} \frac{j\kappa Z_0 e^{j\kappa \Vert {\bf r} \Vert}}{4\pi \Vert {\bf r} \Vert}\left[ \left( {\bf I}-\hat{\bf r}\hat{\bf r}^H \right)+ \frac{j}{\kappa\Vert {\bf r} \Vert}\left( {\bf I}-3\hat{\bf r}\hat{\bf r}^H \right)\right.\notag\\ {} & {} \left. -\frac{1}{(\kappa \Vert {\bf r} \Vert)^2}\left( {\bf I}-3\hat{\bf r}\hat{\bf r}^H \right) \right]\label{green}\\ \simeq {} & {} \varphi_0 \frac{e^{-j\kappa \Vert {\bf r}\Vert}}{\Vert{\bf r}\Vert} \left( {\bf I}-\hat{\bf r}\hat{\bf r}^H \right),\notag \end{align}
很显然,格林函数在天线近场之外的区域内时高次项的影响甚微,忽略后就是我们常用的球面波模型。这里为了简化分析只考虑其中一个极化方向,则阵列响应可以改写为
\begin{equation} {g}({\bf r}_{\rm T},{\bf r}_{\rm R}) = \varphi_0 \frac{e^{-j\kappa \Vert {\bf r}\Vert}}{\Vert{\bf r}\Vert}. \label{eq:sv} \end{equation}
若两侧均为ULA阵列,那么简单的直射径信道可以建模为
\begin{equation} \begin{aligned} \mathbf{H}_{\rm LoS}[:,m] &= {\mathbf g}_{\rm R}({\bf r}_{\rm T}^{(m)})\\&= \left[ \tilde{g}({\bf r}_{\rm T}^{(m)},{\bf r}_{\rm R}^{(1)}),\cdots,\tilde{g}({\bf r}_{\rm T}^{(m)},{\bf r}_{\rm R}^{(N_{\rm R})}) \right]^{T}, \end{aligned} \label{eq:LoS} \end{equation}
其中通过定义\(\tilde{g}(\cdot) = g(\cdot)/\varphi_0\)我们忽略了常量\(\varphi_0\)造成的影响。这里先考虑简单的莱斯信道,那么有
\begin{equation} {\bf H} = \sqrt{\frac{K}{1+K}}\mathbf{H}_{\rm LoS} + \sqrt{\frac{1}{1+K}}\mathbf{H}_{\rm NLoS}, \label{eq:channelmodel} \end{equation}
为方便起见定义
\begin{equation} \begin{aligned} {\bf W}^{(t)} &= ({\bf W}_{\rm RF}^{(t)}{\bf W}_{\rm BB}^{(t)})^H\\ {\bf f}^{(t)} &= {\bf F}_{\rm RF}^{(t)}{\bf F}_{\rm BB}^{(t)}{\bf s}^{(t)} \end{aligned} \end{equation}
那么单次观测模型就可以写作
\begin{equation} {\bf y}^{(t)} = \left( ({\bf f}^{(t)})^{T}\otimes {\bf W}^{(t)} \right){\rm vec}({\bf H})+\tilde{\bf n}^{(t)} \end{equation}
将多次观测叠加之后就有了
\begin{equation} {\bf y} = {\boldsymbol{\Phi}{\bf h}}+\tilde{\bf n}, \label{eq:linearproblem} \end{equation}
那么简单来说优化问题可以写作
\begin{equation} \begin{aligned} {\rm(P1)}\quad\quad\underset{\tilde{\bf h}}{\min}\ &\ \Vert \tilde{\bf h} \Vert_0\\ {\rm s.t.}\ &\ \Vert\boldsymbol{\Phi} \boldsymbol{\Psi} \tilde{\bf h}-\mathbf{y}\Vert_2 \leq \varepsilon, \end{aligned} \end{equation}
该问题的求解并不困难,目前也已经有许多文献介绍,主要方法就是优化放缩,贪婪迭代或者贝叶斯推断。贪婪迭代是一种折中复杂度与性能的方法,一般实现方式为字典匹配。但是近场字典的设计是个关键问题,因此我们提出如下解决方案。
提出方案
对近场信道求解自相关矩阵得到
\begin{equation} \begin{aligned} {\bf R}_{\rm T} & \overset{~~~}{=} \mathbb{E}\left[{\bf H}^{H} {\bf H}\right]\\ & \overset{~~~}{=} \frac{K}{1+K}{\bf H}_{\rm LoS}^{H}{\bf H}_{\rm LoS}+\frac{1}{1+K}\mathbb{E}\left[ {\bf H}_{\rm NLoS}^{H}{\bf H}_{\rm NLoS} \right]\\ &\overset{~~~}{=} \gamma K{\bf H}_{\rm LoS}^{H}{\bf H}_{\rm LoS}+\gamma{\bf I}, \end{aligned} \label{eq:autocorr} \end{equation}
其中的每一个元素可以表示为
\begin{equation} \begin{aligned} {\bf R}_{\rm T}[m^\prime,m] &= \gamma K{\mathbf g}_{\rm R}^H({\bf r}_{\rm T}^{(m)}){\mathbf g}_{\rm R}({\bf r}_{\rm T}^{(m)})+\gamma {1}_{m,m^\prime}\\&=\gamma {1}_{m,m^\prime}+\gamma K\sum_{n=1}^{N_{\rm R}}\frac{e^{-j\kappa \Vert{\bf r}_{\rm T}^{(m)}-{\bf r}_{\rm R}^{(n)}\Vert }}{\Vert{\bf r}_{\rm T}^{(m)}-{\bf r}_{\rm R}^{(n)}\Vert} \\ &\quad\times\frac{e^{j\kappa \Vert{\bf r}_{\rm T}^{(m^\prime)}-{\bf r}_{\rm R}^{(n)}\Vert}}{\Vert{\bf r}_{\rm T}^{(m^\prime)}-{\bf r}_{\rm R}^{(n)}\Vert}, \end{aligned} \label{eq:autocorr2} \end{equation}
做一点小小的近似可以得到
\begin{align} {\bf R}_{\rm T}[m^\prime,m] \approx &~ \gamma {1}_{m,m^\prime}\notag\\&~ +\frac{\gamma K}{r_0^2}\sum_{n=1}^{N_{\rm R}}e^{-j\kappa\frac{\left(x_{\rm T}^{(m)}-x_{\rm R}^{(n)}\right)^2-\left(x_{\rm T}^{(m^\prime)}-x_{\rm R}^{(n)}\right)^2}{2y_0}}\notag\\ =&~\gamma {1}_{m,m^\prime}+\frac{\gamma K e^{j\kappa \frac{(x_{\rm T}^{(m^\prime)})^2-(x_{\rm T}^{(m)})^2}{2y_0}}}{r_0^2 } \label{eq:dft}\\ &~\times\sum_{n=1}^{N_{\rm R}} e^{j\kappa\frac{x_{\rm R}^{(n)}\left(x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)}\right)}{y_0} }\notag\\ \triangleq&~\gamma {1}_{m,m^\prime}+\gamma K e^{j\kappa \frac{(x_{\rm T}^{(m^\prime)})^2-(x_{\rm T}^{(m)})^2}{2y_0}} {\bf R}^\prime_{\rm T}[m^\prime,m],\notag \end{align}
然后对该矩阵做EVD分解容易知道
\begin{equation} {\bf R}_{\rm T}{\bf v}_m = {\bf D}_{\rm T}^{-1} \left( \gamma K\mathbf{R}^\prime_{\rm T}+\gamma {\bf I} \right){\bf D}_{\rm T}{\bf v}_m = \lambda_m{\bf v}_m, \label{eq:evd} \end{equation}
其中我们剥离了有位置属性的参数
\begin{equation} {\bf D}_{\rm T} = {\rm diag}(e^{j\kappa \frac{(x_{\rm T}^{(1)})^2}{2y_0}},\cdots,e^{j\kappa \frac{(x_{\rm T}^{(N_{\rm T})})^2}{2y_0}}). \label{eq:compensation} \end{equation}
但是对EVD的结果并不影响。容易知道这时的相关矩阵中元素可以表示为
\begin{equation} \begin{aligned} {\bf R}_{\rm T}^\prime[m^\prime,m] & \overset{~~~}{=} \frac{1}{r_0^2} \sum_{n=1}^{N_{\rm R}} e^{j\kappa\frac{x_{\rm R}^{(n)}\left(x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)}\right)}{y_0} }\\ &\overset{(a)}{\approx} \frac{1}{r_0^2} \int_{-L_{\rm R}/2}^{L_{\rm R}/2}e^{\frac{j\kappa}{y_0}x (x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)})} {\rm d}x \\&\overset{~~~}{=}\frac{ 2y_0\sin\left[ \frac{\kappa L_{\rm R} (x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)} )}{2y_0} \right] }{ r_0^2 \kappa \left(x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)} \right)}\\ &\overset{~~~}{\propto}\frac{\sin\left[2\pi W (x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)}) \right] }{ \left(x_{\rm T}^{(m)}-x_{\rm T}^{(m^\prime)} \right)}, \end{aligned} \label{eq:toeplitzmat} \end{equation}
该形式恰好是Sinc函数的形式,那么我们据此可以快速计算字典。实际上这个字典恰好是DPSS序列,该序列更存在快速算法实现,此处并不展开。
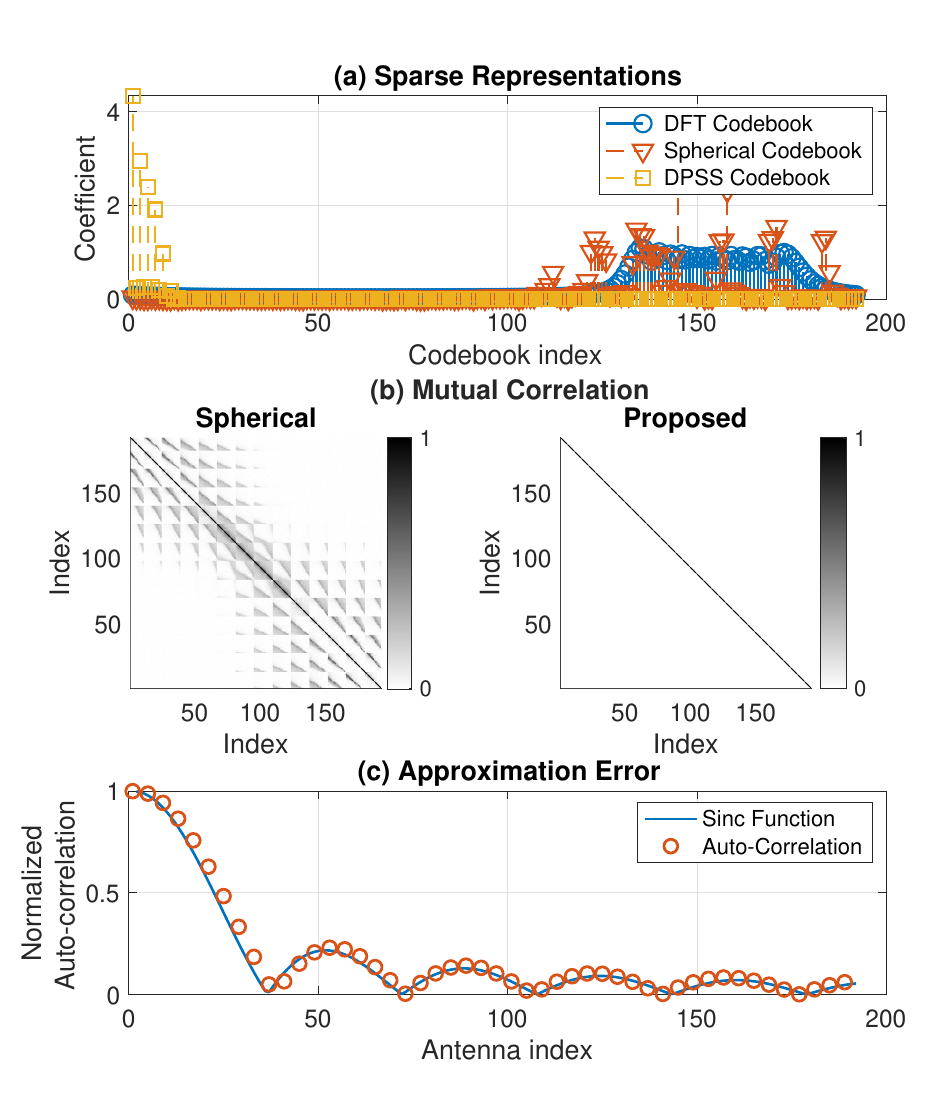
字典设计的方法总结如图
部分仿真结果
该仿真结果主要证明,该码本的稀疏化效果较好(相比DFT和极坐标),正交性高,且过程中的近似可以视作无误差。
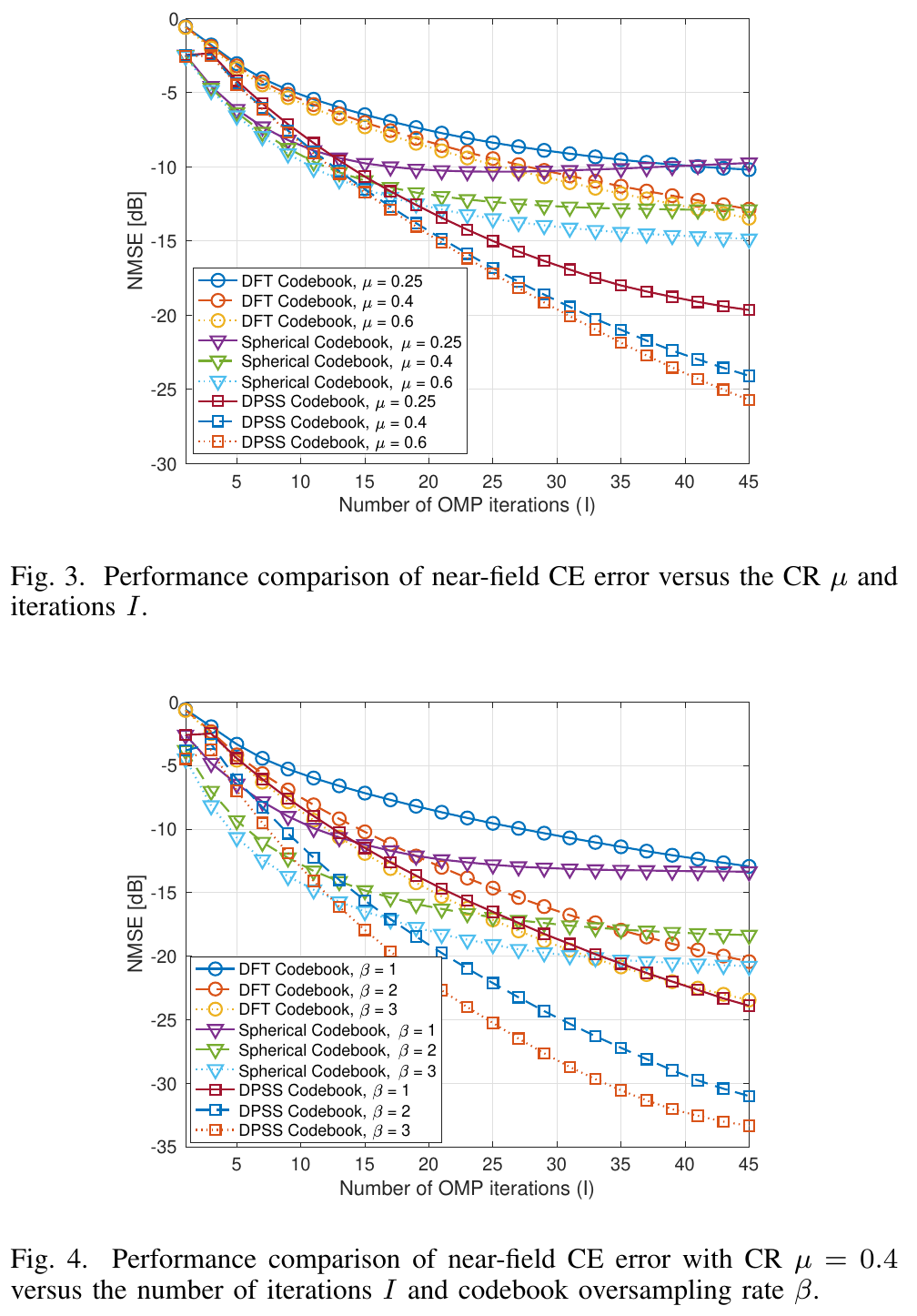
这两个图主要比较不同采样数和不同码本冗余倍数下的差异。结论显然,不再赘述。
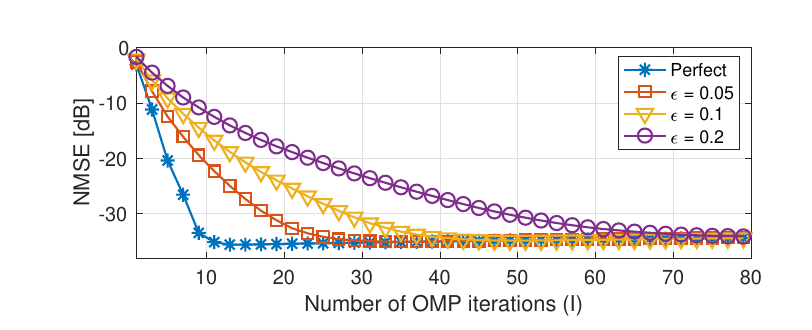
该图展示估计误差在不同范围时的收敛性。
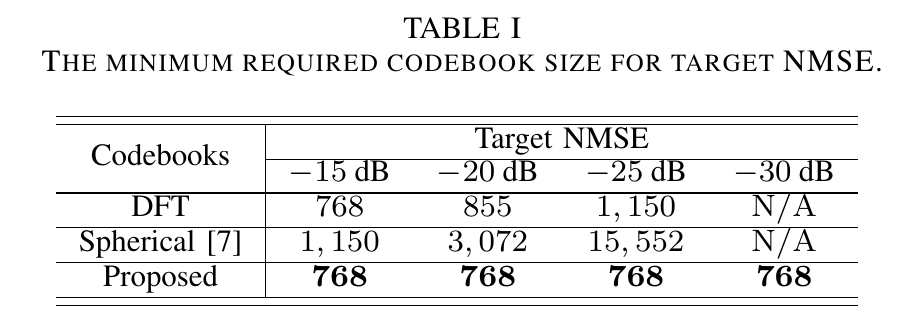
最后表格比较了一下 如果想要达到指定性能,需要多大的码本。