Shicong LIU

Shicong LIU

Ph.D. Candidate, HKPFS Awardee, Amateur Film Photographer

分块环形阵列的一些基本特性
Study on Sectored Circular Arrays

2 minutes read

Published:

Translation Provider: Google

今天我们一篇关于分扇区的环形阵列的工作在Globecom展示，收获了许多专家学者的建议，我们对此表示衷心的感谢。该工作的可复现仿真与演示文稿可以在我们的GitHub上公开获取。

背景

近场相关的工作近年来已经越来越多，相信此处我们不需要提供过多的背景介绍。不过大部分的工作都是基于线性(或者平面)阵列的，而实际上平面阵列在许多问题上并不能达到最优。在一些近场通信的研究中我们不难找到，近场信道的角度和距离这两个参数的估计误差并不相同1，如图

参数估计的CRB

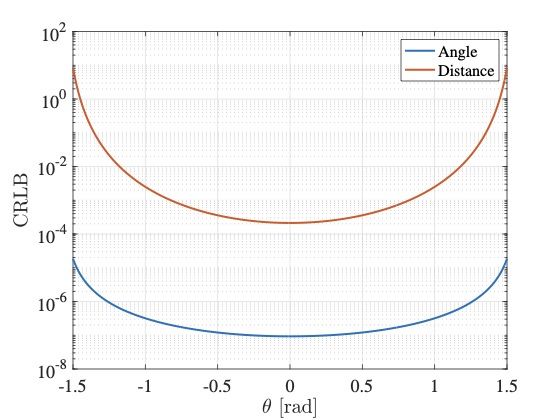
这个图主要展示了两种缺陷，首先线性阵列在两侧可能出现“崩边”现象，边缘分辨率随着等效孔径剧烈崩溃；其次，距离估计的误差可能远高于角度估计，即使角度估计精准，距离误差也会导致定位失误。出现这个现象可以理解为线性阵列的空间特性，因此我们或许应该考虑尝试其他阵列结构。

目前也有一些其他工作在考虑环形阵列的可能应用，除了我在文章intro部分提出的问题之外，实际上还有QMUL Zhaolin Wang等人的工作，值得学习。

💡 会后咨询了一位在华为的研究员，他表示目前无论是非均匀还是非线性的天线，都有比较高的制作难度，目前来看商用的机会还不大。

技术说明

本文假设的系统模型非常简单，一个分扇区的环形阵列与近场区用户，环境内存在若干散射体。

系统模型

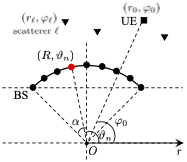
这里的接收信号模型可以表示为

$$ \begin{equation} \begin{aligned} \mathbf{h}_k[n] =\frac{1}{\sqrt{N L}} \sum_{\ell=0}^L \frac{\alpha_{\ell} e^{\jmath \frac{2 \pi}{c} f_k\left(d_{\ell}+d_{\ell, n}\right)}}{d_{\ell} d_{\ell, n}} =\sum_{\ell=0}^L \frac{\tilde{\alpha}_{k, \ell} e^{\jmath \frac{2 \pi}{c} f_k d_{\ell, n}}}{d_{\ell, n}}, \end{aligned} \end{equation} $$

这个信号也可以说是“波前(wavefront)”。其中距离项我们会做简单的近似如下

$$ \begin{equation} d_{\ell,n} = \sqrt{r_{\ell}^2+R^2-2Rr_{\ell} \cos\left( \vartheta_n-\varphi_\ell \right) }\approx r_\ell +\frac{R^2}{2r_\ell}-R\cos\left( \vartheta_n - \varphi_\ell \right) \label{eq:distance1} \end{equation} $$

被记录的波前可以被用于反向电磁传播模拟如下

$$ \begin{equation} \begin{aligned} F_k(r, \varphi) &=\sum_{n=1}^N \underbrace{\mathbf{y}_k[n] s_k^*}_{\rm Wavefront}~\underbrace{e^{-\jmath \frac{2 \pi}{c} f_k d_n}}_{\rm Propag.} =\sum_{\ell=0}^L \sum_{n=1}^N \frac{\tilde{\alpha}_{k, \ell} e^{\jmath \frac{2 \pi}{c} f_k\left(d_{\ell, n}-d_n\right)}}{d_{\ell, n}}+\tilde{\mathbf{n}}_k\\ &\triangleq \sum_{\ell=0}^L F_k^{(\ell)}(r, \varphi)+\tilde{\mathbf{n}}_k \label{eq:emu} \end{aligned} \end{equation} $$

其中第一个算式里面的Propag.用于模拟电磁传输。这个函数也被称为模糊函数，用于描述重建的分辨率。

对于这个模糊函数我们有两个基本结论。这可以在我们的期刊版论文2中找到，主要可以概括为

  1. 模糊函数只在目标坐标位置取最大值。
  2. 模糊函数在特定的渐进条件下趋近于\(0\)，从而产生干净的重建结果。

如图所示的重建例子可以很好地说明这一点

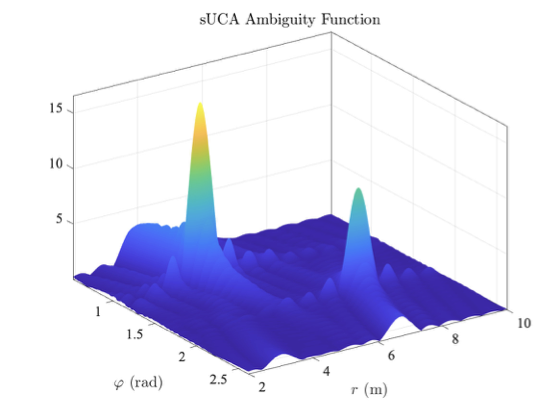
分别位于\(\displaystyle(4,\frac{\pi}{3})\) 和 \(\displaystyle(7,\frac{7\pi}{12})\) 的两个目标

这个重建的过程实际上可以转化为卷积运算，从而让我们可以使用快速傅里叶变换来实现快速重建。

简要结论

经过对模糊函数的分析，我们容易证明，环形结构的阵列能够实现较好的边缘分辨率，实际上，是平稳的分辨率过渡————角度分辨率几乎与位置无关。

对于距离分辨率，结果实际上并没有令人满意。环形阵列的距离分辨率与线性阵列相似————在BP算法下都没有距离分辨率。

此外，环形阵列由于采用和线性阵列相同的总孔径，性能的优势并不显著。环形阵列的等效孔径将远小于线性阵列，因此角度分辨率实际低于线性阵列，至少在正前方位置。这样的结果还导致了近场范围的缩小，这使得拥有高自由度的区域剧烈收缩，影响通信效率。

Zhaolin的工作则考虑了等效孔径相同，因此环形阵列的性能优势可以完全凸显。经过仿真我们容易知道间距较大的时候环形阵列的sidelobe仍然是可接受的，因此在这种情况下考虑环形阵列十分合适。

我对我固执于相同孔径的意见有些后悔，也十分推荐这篇让我意识到这一点的论文。

部分仿真结果

一些仿真结果

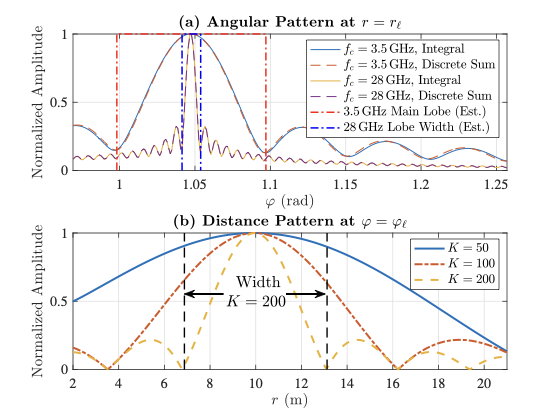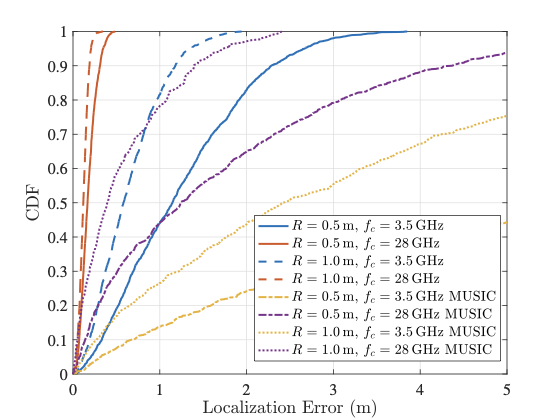如有问题记得邮箱联系:-)

参考文献

  1. H. Wang, Z. Xiao and Y. Zeng, “Cramér-Rao Bounds for Near-Field Sensing With Extremely Large-Scale MIMO,” IEEE Transactions on Signal Processing, vol. 72, pp. 701-717, 2024. ↩

  2. Shicong Liu, Xianghao Yu, Zhen Gao, Jie Xu, Derrick Wing Kwan Ng, Shuguang Cui, “Sensing-Enhanced Channel Estimation for Near-Field XL-MIMO Systems”, IEEE J. Sel. Areas Commun. ↩